イラスト 尼崎西高校 藺牟田綾花
自然界を支配する不思議な数列 HOME 戻る

イラスト 尼崎西高校 藺牟田綾花
|
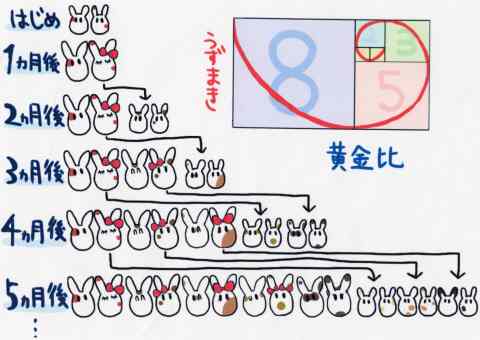
「オスとメスの1対の子ウサギが、1ヶ月後に大人になり、メスはその1ヶ月後から毎月1対のウサギを産み続けると、1年後にはウサギは何対になっていますか?」 今年の干支にちなんだ問題ですが、これは1200年頃に活躍したイタリアの数学者フィボナッチが、インドの優れた数学を紹介した著書の中で解説した問題で、ウサギは1ヶ月毎に、1、1、2、3、5、8、13、21、34、55、89、144、233対というふうに増えてゆきます。 この数の並びは、1+1=2、1+2=3、2+3=5と、前2つの数を足した答を並べた数列になり、インドでは6世紀頃から知られていたそうですが、ヨーロッパに紹介した彼の名をとって「フィボナッチ数列」と呼ばれるようになりました。 そしてウサギを用いた数遊びで、一見半端な数が並んでいるようですが、不思議なことに、たとえば多くの植物の花びらの数は、ユリが3枚、サクラやウメは5枚、コスモスや8枚で、「好き、嫌い、好き、・・・」と花びらをちぎってゆく恋占いに使われるマーガレットやガーベラなどのキク科の花びらも、13枚、21枚、34枚、55枚などが多く、ほとんどがフィボナッチ数と一致します。 また、花びらは葉が進化したものなので、植物の葉も、茎を中心にして、2方向、3方向、5方向、8方向というように生えています。葉を重ねずに日陰を少なくして光合成の効率を上げるには、フィボナッチ数が適しているようなのです。 さらに自然界を見ると、ヒトデは5角形ですし、松ぼっくりのうろこやヒマワリのタネも渦巻き状に並んでいて、その本数はフィボナッチ数に一致します。 次に、フィボナッチ数を一辺の長さにした正方形を並べて曲線を描くと、カタツムリやオウムガイなどの渦巻きができます。また、この作図でできる長方形の辺の長さの比、つまり連続するフィボナッチ数の比は、数が大きくなると1対1.618に近づきます。これは黄金比と呼ばれ、私たちが安定感や美しさを感じる比率として古くから知られ、古代ギリシャのパルテノン神殿の高さと横幅の比率や、ミロのヴィーナスの体の各部の比率に一致します。 さらに、株価や為替の反発もフィボナッチ数に関係しているといわれます。 自然界はフィボナッチ数であふれ、自然を支配したつもりの私たちヒトもまた、その深層心理がこの不思議な数列に支配されているのかもしれません。 |
※この文章は、生物Iの授業で話した内容をまとめたものです。
化学教育兵庫サークルに校正、編集していただき、2011年1月に神戸新聞「理科の散歩道」に掲載されました。
Ikimono-Note by E.Yoshida